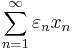Unconditional convergence

In mathematical analysis, a series 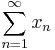$\sum_{n=1}^\infty x_n$ in a Banach space X is unconditionally convergent if for every permutation 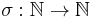$\sigma: \mathbb N \to \mathbb N$ the series 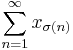$\sum_{n=1}^\infty x_{\sigma(n)}$ converges.

This notion is often defined in an equivalent way: A series is unconditionally convergent if for every sequence 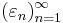$(\varepsilon_n)_{n=1}^\infty$ , with 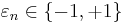$\varepsilon_n\in\{-1, %2B1\}$ , the series

$\sum_{n=1}^\infty \varepsilon_n x_n$

converges.

Every absolutely convergent series is unconditionally convergent, but the converse implication does not hold in general. When X = Rⁿ, then, by the Riemann series theorem, the series 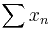$\sum x_n$ is unconditionally convergent if and only if it is absolutely convergent.

References

Ch. Heil: A Basis Theory Primer
K. Knopp: "Theory and application of infinite series"
K. Knopp: "Infinite sequences and series"
P. Wojtaszczyk: "Banach spaces for analysts"

This article incorporates material from Unconditional convergence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Unconditional convergence

See also

References